Memahami Keindahan Simetri dan Pencerminan

Memahami Keindahan Simetri dan Pencerminan

Dalam dunia matematika, terdapat konsep-konsep yang tidak hanya membangun pemahaman logis, tetapi juga mengajarkan kita untuk melihat keindahan dalam pola dan bentuk. Salah satu konsep yang sangat menarik dan mudah dipahami oleh siswa kelas 4 SD adalah simetri dan pencerminan. Materi ini seringkali menjadi bagian penting dalam pelajaran Geometri di tingkat dasar, karena tidak hanya memperkenalkan sifat-sifat bangun datar, tetapi juga melatih kemampuan spasial dan observasi anak. Mari kita selami lebih dalam mengenai simetri dan pencerminan bangun datar, lengkap dengan contoh-contoh yang relevan untuk siswa kelas 4.

Garis Besar Artikel:

  1. <p><strong>Memahami Keindahan Simetri dan Pencerminan</strong></p> <p>” title=”</p> <p><strong>Memahami Keindahan Simetri dan Pencerminan</strong></p> <p>“></p> <p><strong>Pendahuluan: Apa Itu Simetri dan Pencerminan?</strong></p> <ul> <li>Pengertian sederhana simetri.</li> <li>Pengertian sederhana pencerminan.</li> <li>Hubungan antara simetri dan pencerminan.</li> </ul> </li> <li> <p><strong>Mengenal Simetri Putar (Rotational Symmetry)</strong></p> <ul> <li>Definisi simetri putar.</li> <li>Cara mengidentifikasi simetri putar.</li> <li>Contoh bangun datar dengan simetri putar.</li> <li>Tingkat simetri putar.</li> </ul> </li> <li> <p><strong>Mengenal Simetri Lipat (Reflectional Symmetry)</strong></p> <ul> <li>Definisi simetri lipat.</li> <li>Garis simetri sebagai cermin.</li> <li>Cara mengidentifikasi garis simetri.</li> <li>Contoh bangun datar dengan simetri lipat.</li> <li>Jumlah garis simetri.</li> </ul> </li> <li> <p><strong>Pencerminan Bangun Datar</strong></p> <ul> <li>Konsep pencerminan sebagai bayangan.</li> <li>Pencerminan terhadap garis tertentu (horizontal, vertikal, diagonal).</li> <li>Sifat-sifat hasil pencerminan (ukuran, bentuk, jarak).</li> <li>Contoh penerapan pencerminan dalam kehidupan sehari-hari.</li> </ul> </li> <li> <p><strong>Latihan dan Contoh Soal untuk Kelas 4 SD</strong></p> <ul> <li>Soal identifikasi simetri lipat dan putar.</li> <li>Soal menggambar hasil pencerminan.</li> <li>Soal cerita sederhana terkait simetri dan pencerminan.</li> </ul> </li> <li> <p><strong>Kesimpulan: Mengapa Simetri dan Pencerminan Penting?</strong></p> <ul> <li>Manfaat memahami konsep ini.</li> <li>Keterkaitan dengan seni dan alam.</li> </ul> </li> </ol> <p><strong>Memahami Keindahan Simetri dan Pencerminan</strong></p> <p>Dunia di sekitar kita penuh dengan pola yang menarik dan teratur. Pernahkah kalian memperhatikan kupu-kupu yang sayapnya terlihat sama di kedua sisi? Atau sebuah jam dinding yang angka-angkanya tersusun rapi? Keindahan seperti ini seringkali berkaitan dengan konsep matematika yang disebut simetri dan pencerminan. Bagi siswa kelas 4 SD, memahami kedua konsep ini akan membuka mata terhadap detail-detail menarik dalam bentuk dan bangun datar yang sering kita jumpai.</p> <p><strong>1. Pendahuluan: Apa Itu Simetri dan Pencerminan?</strong></p> <p>Mari kita mulai dengan pengertian yang paling sederhana.</p> <ul> <li><strong>Simetri</strong> adalah keadaan atau sifat di mana suatu objek terlihat sama ketika diputar atau dicerminkan. Bayangkan sebuah objek yang jika kita potong menjadi dua bagian, kedua bagian tersebut akan saling cocok sempurna. Itulah inti dari simetri.</li> <li><strong>Pencerminan</strong> lebih mudah dibayangkan dengan menggunakan cermin. Ketika kita berdiri di depan cermin, kita melihat bayangan diri kita yang persis sama. Dalam matematika, pencerminan adalah proses mengubah posisi suatu objek seolah-olah dipantulkan oleh sebuah cermin. Objek yang dicerminkan akan memiliki bentuk dan ukuran yang sama, tetapi posisinya berlawanan arah.</li> </ul> <div style=
    See also  Konversi Word ke PDF di Office 2013: Panduan Lengkap

Hubungan antara simetri dan pencerminan sangat erat. Simetri lipat, misalnya, adalah jenis simetri yang dicapai melalui pencerminan. Sebuah bangun datar dikatakan memiliki simetri lipat jika ia dapat dibagi menjadi dua bagian yang sama persis oleh sebuah garis, di mana kedua bagian tersebut akan saling menutupi jika dilipat di sepanjang garis tersebut.

2. Mengenal Simetri Putar (Rotational Symmetry)

Selain simetri lipat, ada juga simetri putar.

  • Definisi Simetri Putar: Simetri putar terjadi ketika sebuah bangun datar dapat diputar mengelilingi titik pusatnya sejauh kurang dari satu putaran penuh (360 derajat) dan hasil putarannya akan kembali menempati posisi semula.
  • Cara Mengidentifikasi Simetri Putar: Untuk menemukannya, kita bisa mencoba memutar bangun datar tersebut. Jika setelah diputar sedikit saja (misalnya 90 derajat, 120 derajat, atau 180 derajat), bangun tersebut terlihat persis sama seperti sebelum diputar, maka bangun itu memiliki simetri putar. Kita perlu memperhatikan berapa kali posisi semula tercapai dalam satu putaran penuh.
  • Contoh Bangun Datar dengan Simetri Putar:
    • Persegi: Persegi memiliki simetri putar tingkat 4. Ini berarti ia dapat menempati posisi semula sebanyak 4 kali dalam satu putaran penuh. Ia terlihat sama ketika diputar 90°, 180°, dan 270°.
    • Persegi Panjang: Persegi panjang memiliki simetri putar tingkat 2. Ia terlihat sama ketika diputar 180°.
    • Lingkaran: Lingkaran memiliki simetri putar tak terhingga. Ia akan terlihat sama di setiap sudut putaran.
    • Segitiga Sama Sisi: Segitiga sama sisi memiliki simetri putar tingkat 3. Ia terlihat sama ketika diputar 120° dan 240°.
    • Jajar Genjang: Jajar genjang memiliki simetri putar tingkat 2. Ia terlihat sama ketika diputar 180°.
    • Belah Ketupat: Belah ketupat memiliki simetri putar tingkat 2. Ia terlihat sama ketika diputar 180°.
  • Tingkat Simetri Putar: Tingkat simetri putar adalah jumlah kali bangun datar tersebut menempati posisi semula dalam satu putaran penuh (360 derajat).

3. Mengenal Simetri Lipat (Reflectional Symmetry)

Simetri lipat adalah konsep yang paling sering dihubungkan dengan "kesamaan" pada kedua sisi.

  • Definisi Simetri Lipat: Simetri lipat adalah ketika sebuah bangun datar dapat dibagi menjadi dua bagian yang sama persis oleh sebuah garis lurus. Jika kita melipat bangun datar tersebut di sepanjang garis ini, kedua bagiannya akan saling menutupi dengan sempurna.
  • Garis Simetri sebagai Cermin: Garis yang membagi bangun datar menjadi dua bagian yang sama persis ini disebut garis simetri. Garis simetri ini bertindak seperti cermin. Bagian di satu sisi garis simetri adalah bayangan cermin dari bagian di sisi lainnya.
  • Cara Mengidentifikasi Garis Simetri: Untuk menemukan garis simetri, kita bisa mencoba menggambar garis lurus di berbagai arah pada bangun datar. Jika garis tersebut membagi bangun menjadi dua bagian yang jika dilipat saling menutupi, maka itu adalah garis simetri.
  • Contoh Bangun Datar dengan Simetri Lipat:
    • Persegi: Memiliki 4 garis simetri. Dua garis simetri horizontal dan vertikal yang melalui titik tengah, serta dua garis simetri diagonal.
    • Persegi Panjang: Memiliki 2 garis simetri, yaitu garis horizontal dan vertikal yang melalui titik tengahnya.
    • Lingkaran: Memiliki tak terhingga garis simetri. Setiap garis yang melewati titik pusat lingkaran adalah garis simetri.
    • Segitiga Sama Sisi: Memiliki 3 garis simetri, masing-masing ditarik dari setiap sudut ke titik tengah sisi di hadapannya.
    • Segitiga Sama Kaki: Memiliki 1 garis simetri, yaitu garis yang membagi dua sisi yang sama panjang.
    • Segitiga Sembarang: Tidak memiliki garis simetri.
    • Belah Ketupat: Memiliki 2 garis simetri, yaitu kedua diagonalnya.
    • Trapesium Sama Kaki: Memiliki 1 garis simetri, yaitu garis yang menghubungkan titik tengah sisi sejajar.
    • Layang-layang: Memiliki 1 garis simetri, yaitu diagonal yang membagi dua sudut yang sama besar.
  • Jumlah Garis Simetri: Setiap bangun datar mungkin memiliki jumlah garis simetri yang berbeda, bahkan ada yang tidak memiliki sama sekali.
See also  Sedekah: Indahnya Berbagi Kebaikan

4. Pencerminan Bangun Datar

Pencerminan adalah cara kita membuat bayangan dari sebuah bangun datar.

  • Konsep Pencerminan sebagai Bayangan: Ketika sebuah bangun datar dicerminkan, ia akan menghasilkan bayangan yang ukurannya sama persis. Namun, orientasi atau arahnya akan terbalik. Bayangkan kamu melihat dirimu di cermin, tangan kananmu terlihat seperti tangan kiri di cermin.
  • Pencerminan terhadap Garis Tertentu: Kita bisa mencerminkan bangun datar terhadap berbagai jenis garis:
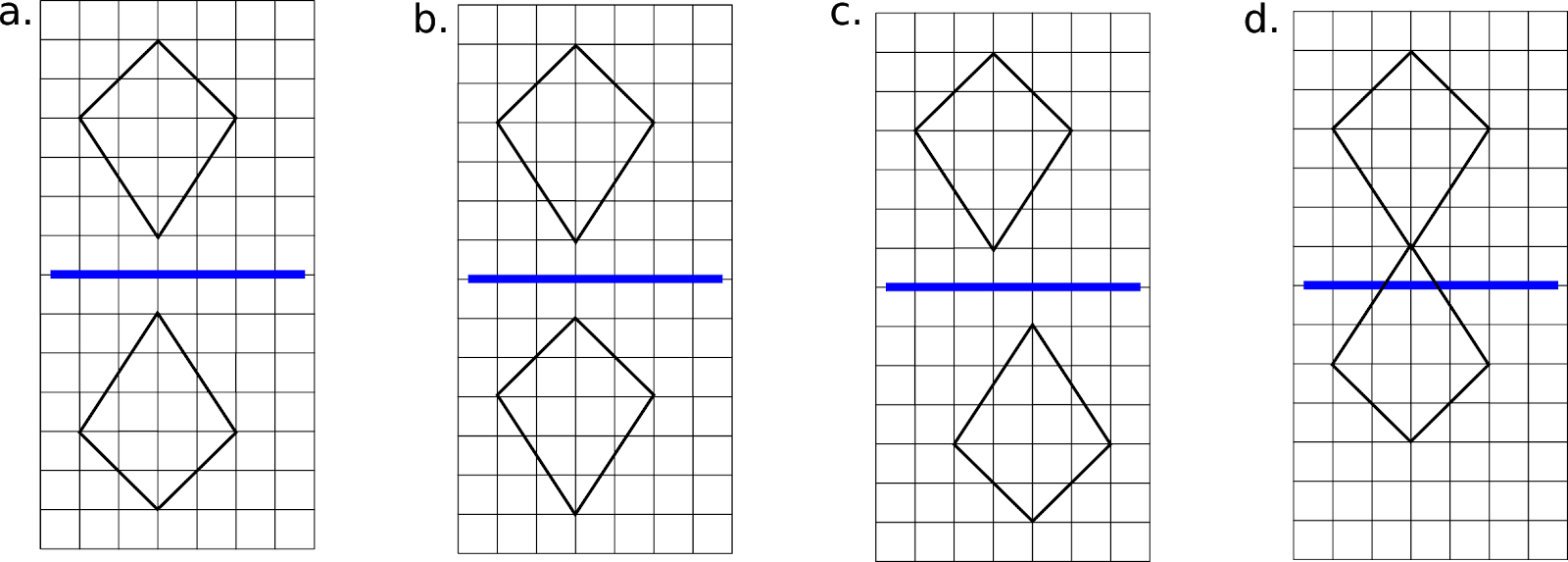
    • Pencerminan terhadap Garis Horizontal: Jika garis cerminnya horizontal, maka bayangannya akan terbalik atas-bawah.
    • Pencerminan terhadap Garis Vertikal: Jika garis cerminnya vertikal, maka bayangannya akan terbalik kiri-kanan.
    • Pencerminan terhadap Garis Diagonal: Jika garis cerminnya miring (diagonal), maka bayangannya akan terbalik secara diagonal pula.
  • Sifat-sifat Hasil Pencerminan:
    • Ukuran: Ukuran bangun datar asli dan bayangannya selalu sama.
    • Bentuk: Bentuk bangun datar asli dan bayangannya selalu sama.
    • Jarak: Jarak setiap titik pada bangun datar asli ke garis cermin sama dengan jarak bayangannya ke garis cermin.
  • Contoh Penerapan Pencerminan dalam Kehidupan Sehari-hari:
    • Cermin di Kamar Mandi: Ini adalah contoh paling jelas. Wajah kita di cermin adalah hasil pencerminan.
    • Pantulan di Air: Bayangan perahu atau pohon di permukaan air adalah hasil pencerminan.
    • Desain Bangunan: Banyak arsitektur bangunan yang menggunakan prinsip simetri dan pencerminan untuk menciptakan keindahan dan keseimbangan.
    • Logo Perusahaan: Beberapa logo perusahaan dirancang dengan simetri agar terlihat menarik dan mudah diingat.

5. Latihan dan Contoh Soal untuk Kelas 4 SD

Untuk memperkuat pemahaman, mari kita coba beberapa contoh soal:

Contoh Soal 1: Identifikasi Simetri Lipat

Perhatikan bangun datar berikut: Persegi, Persegi Panjang, Segitiga Sama Sisi, Segitiga Sama Kaki, Lingkaran.

  • Manakah dari bangun datar tersebut yang memiliki 4 garis simetri? (Jawaban: Persegi)
  • Manakah yang memiliki 1 garis simetri? (Jawaban: Segitiga Sama Kaki)
  • Manakah yang memiliki tak terhingga garis simetri? (Jawaban: Lingkaran)
  • Gambarkan garis-garis simetri pada bangun datar persegi.
See also  Soal Bahasa Inggris Kelas 7: Bab 4 (Things Around Us)

Contoh Soal 2: Identifikasi Simetri Putar

Perhatikan bangun datar berikut: Persegi, Persegi Panjang, Jajar Genjang, Segitiga Sama Sisi.

  • Manakah dari bangun datar tersebut yang memiliki simetri putar tingkat 2? (Jawaban: Persegi Panjang, Jajar Genjang)
  • Manakah yang memiliki simetri putar tingkat 4? (Jawaban: Persegi)
  • Jika sebuah bangun datar memiliki simetri putar tingkat 3, berapa derajat minimal ia harus diputar agar kembali ke posisi semula? (Jawaban: 120 derajat)

Contoh Soal 3: Menggambar Hasil Pencerminan

Diberikan sebuah bangun datar (misalnya segitiga) dan sebuah garis cermin. Siswa diminta menggambar bayangan segitiga tersebut setelah dicerminkan terhadap garis cermin yang diberikan (misalnya garis vertikal).

  • Soal: Gambar bayangan segitiga ABC di bawah ini jika dicerminkan terhadap garis m.
    (Di sini guru akan menggambar segitiga dan garis cerminnya, lalu siswa menggambar bayangannya)

Contoh Soal 4: Soal Cerita Sederhana

  • "Ibu membuat taplak meja berbentuk persegi. Berapa banyak cara Ibu bisa memotong taplak meja tersebut menjadi dua bagian yang sama persis dengan satu kali guntingan lurus dari satu sisi ke sisi lain?" (Jawaban: 4 cara, yaitu garis simetri persegi)
  • "Adik menggambar kupu-kupu. Ia menggambar satu sisi sayapnya. Jika ia ingin menggambar sisi satunya lagi agar terlihat sama persis, ia perlu menggunakan prinsip apa?" (Jawaban: Pencerminan atau simetri lipat)

6. Kesimpulan: Mengapa Simetri dan Pencerminan Penting?

Memahami konsep simetri dan pencerminan bukan hanya sekadar menghafal rumus atau sifat. Konsep ini memiliki banyak manfaat:

  • Mengembangkan Kemampuan Spasial: Anak-anak menjadi lebih peka terhadap bentuk, posisi, dan orientasi objek di ruang.
  • Meningkatkan Keterampilan Observasi: Anak belajar untuk melihat detail dan pola yang tersembunyi.
  • Dasar untuk Konsep Matematika Lanjutan: Simetri dan pencerminan adalah fondasi penting untuk topik geometri yang lebih kompleks di kemudian hari.
  • Apresiasi Seni dan Alam: Konsep ini membantu anak mengapresiasi keindahan dalam desain seni, arsitektur, pola alam (seperti daun, bunga, atau hewan), dan benda-benda di sekitar mereka.
  • Melatih Kemampuan Pemecahan Masalah: Soal-soal yang melibatkan identifikasi dan pembuatan simetri serta pencerminan melatih anak untuk berpikir logis dan kreatif.

Dengan mempelajari simetri dan pencerminan, siswa kelas 4 SD tidak hanya belajar matematika, tetapi juga belajar melihat dunia dengan cara yang lebih teratur, harmonis, dan penuh keindahan. Ini adalah pelajaran yang menyenangkan dan membuka wawasan!