stiksintcarolus.ac.id

Menguasai Segitiga: Luas dan Keliling untuk Kelas 4

Pendahuluan

Segitiga adalah salah satu bentuk geometri dasar yang sering kita temui dalam kehidupan sehari-hari. Mulai dari atap rumah, potongan pizza, hingga rambu lalu lintas, segitiga hadir di sekitar kita. Memahami konsep luas dan keliling segitiga adalah keterampilan penting bagi siswa kelas 4, karena ini tidak hanya membantu mereka dalam pelajaran matematika, tetapi juga mengembangkan kemampuan berpikir logis dan pemecahan masalah. Artikel ini akan membahas secara mendalam tentang luas dan keliling segitiga, dimulai dari definisi dasar, jenis-jenis segitiga, rumus perhitungan, contoh soal, hingga tips dan trik untuk memudahkan pemahaman.

I. Memahami Dasar Segitiga

• A. Definisi Segitiga:

  Segitiga adalah bangun datar yang dibentuk oleh tiga sisi yang saling berpotongan dan memiliki tiga sudut. Titik pertemuan antara dua sisi disebut dengan titik sudut.

• B. Unsur-Unsur Segitiga:
  • Sisi: Garis yang membentuk segitiga. Segitiga memiliki tiga sisi.
  • Sudut: Daerah yang dibentuk oleh dua sisi yang bertemu di satu titik. Segitiga memiliki tiga sudut. Jumlah ketiga sudut dalam segitiga selalu 180 derajat.
  • Alas: Sisi yang menjadi dasar segitiga. Pemilihan alas bersifat fleksibel, tergantung pada posisi segitiga dan kemudahan perhitungan.
  • Tinggi: Garis tegak lurus yang ditarik dari titik sudut ke alas (atau perpanjangan alas). Tinggi selalu membentuk sudut siku-siku (90 derajat) dengan alas.

• C. Jenis-Jenis Segitiga:

  Segitiga dapat diklasifikasikan berdasarkan panjang sisi dan besar sudutnya. Berikut adalah beberapa jenis segitiga yang umum:

  • Segitiga Sama Sisi: Segitiga yang memiliki tiga sisi yang sama panjang dan tiga sudut yang sama besar (masing-masing 60 derajat).
  • Segitiga Sama Kaki: Segitiga yang memiliki dua sisi yang sama panjang dan dua sudut yang sama besar.
  • Segitiga Siku-Siku: Segitiga yang salah satu sudutnya membentuk sudut siku-siku (90 derajat). Sisi di depan sudut siku-siku disebut hipotenusa.
  • Segitiga Tumpul: Segitiga yang salah satu sudutnya lebih besar dari 90 derajat.
  • Segitiga Lancip: Segitiga yang semua sudutnya kurang dari 90 derajat.
  • Segitiga Sembarang: Segitiga yang semua sisinya berbeda panjang dan semua sudutnya berbeda besar.

II. Keliling Segitiga

• A. Definisi Keliling:

  Keliling adalah total panjang semua sisi pada suatu bangun datar.

• B. Rumus Keliling Segitiga:

  Keliling segitiga dihitung dengan menjumlahkan panjang ketiga sisinya.

  • Keliling = Sisi 1 + Sisi 2 + Sisi 3

  Atau dapat ditulis:

  • K = a + b + c

  Dimana:

  • K = Keliling
  • a, b, c = Panjang sisi-sisi segitiga

• C. Contoh Soal Keliling Segitiga:

  1. Sebuah segitiga memiliki sisi dengan panjang 5 cm, 7 cm, dan 9 cm. Hitunglah keliling segitiga tersebut!

     • Penyelesaian:
       • K = 5 cm + 7 cm + 9 cm
       • K = 21 cm

     Jadi, keliling segitiga tersebut adalah 21 cm.

  2. Sebuah segitiga sama sisi memiliki panjang sisi 8 cm. Berapakah keliling segitiga tersebut?

     • Penyelesaian:
       • Karena segitiga sama sisi, maka ketiga sisinya sama panjang.
       • K = 8 cm + 8 cm + 8 cm
       • K = 24 cm

     Jadi, keliling segitiga sama sisi tersebut adalah 24 cm.

  3. Sebuah taman berbentuk segitiga sama kaki. Dua sisi yang sama panjang masing-masing berukuran 10 meter. Sisi yang lain berukuran 6 meter. Berapakah keliling taman tersebut?

     • Penyelesaian:
       • K = 10 m + 10 m + 6 m
       • K = 26 m

     Jadi, keliling taman tersebut adalah 26 meter.

III. Luas Segitiga

• A. Definisi Luas:

  Luas adalah ukuran seberapa besar permukaan suatu bangun datar.

• B. Rumus Luas Segitiga:

  Luas segitiga dihitung menggunakan rumus:

  • Luas = (1/2) x Alas x Tinggi

  Atau dapat ditulis:

  • L = (1/2) x a x t

  Dimana:

  • L = Luas
  • a = Panjang alas segitiga
  • t = Tinggi segitiga (garis tegak lurus dari titik sudut ke alas)

• C. Contoh Soal Luas Segitiga:

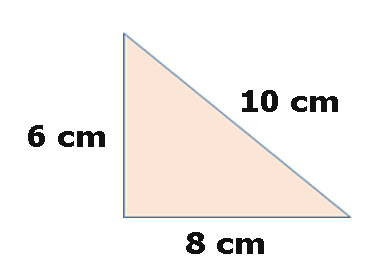
  1. Sebuah segitiga memiliki alas 10 cm dan tinggi 6 cm. Hitunglah luas segitiga tersebut!

     • Penyelesaian:
       • L = (1/2) x 10 cm x 6 cm
       • L = (1/2) x 60 cm²
       • L = 30 cm²

     Jadi, luas segitiga tersebut adalah 30 cm².

  2. Sebuah sapu tangan berbentuk segitiga siku-siku. Alasnya 12 cm dan tingginya 5 cm. Berapakah luas sapu tangan tersebut?

     • Penyelesaian:
       • L = (1/2) x 12 cm x 5 cm
       • L = (1/2) x 60 cm²
       • L = 30 cm²

     Jadi, luas sapu tangan tersebut adalah 30 cm².

  3. Sebuah bendera berbentuk segitiga memiliki alas 80 cm dan tinggi 40 cm. Hitunglah luas bendera tersebut!

     • Penyelesaian:
       • L = (1/2) x 80 cm x 40 cm
       • L = (1/2) x 3200 cm²
       • L = 1600 cm²

     Jadi, luas bendera tersebut adalah 1600 cm².

IV. Tips dan Trik Mengerjakan Soal Segitiga

• A. Menggambar Segitiga:

  Menggambar segitiga (jika belum disediakan) dapat membantu memvisualisasikan soal dan memudahkan identifikasi alas dan tinggi.

• B. Memastikan Satuan:

  Pastikan semua satuan panjang sisi dan tinggi sama sebelum melakukan perhitungan. Jika berbeda, ubah terlebih dahulu ke satuan yang sama.

• C. Memahami Konsep Tinggi:

  Ingatlah bahwa tinggi segitiga selalu tegak lurus dengan alas. Kadang-kadang, tinggi tidak berada di dalam segitiga (terutama pada segitiga tumpul).

• D. Membedakan Alas dan Tinggi:

  Perhatikan dengan seksama mana yang merupakan alas dan mana yang merupakan tinggi. Kesalahan dalam mengidentifikasi alas dan tinggi akan menyebabkan kesalahan dalam perhitungan luas.

• E. Menggunakan Rumus dengan Benar:

  Pastikan rumus yang digunakan sudah benar dan semua nilai yang diperlukan sudah diketahui.

• F. Latihan Soal:

  Semakin banyak latihan soal, semakin terbiasa dengan berbagai tipe soal dan semakin mudah dalam memahami konsep luas dan keliling segitiga.

• G. Menggunakan Alat Bantu:

  Gunakan penggaris dan busur derajat untuk membantu menggambar dan mengukur segitiga.

V. Penerapan Konsep Segitiga dalam Kehidupan Sehari-hari

• A. Arsitektur:

  Segitiga digunakan dalam desain bangunan, jembatan, dan struktur lainnya karena kekuatannya. Atap rumah seringkali berbentuk segitiga.

• B. Desain Produk:

  Segitiga digunakan dalam desain berbagai produk, seperti kemasan makanan, mainan, dan perabotan rumah tangga.

• C. Seni dan Kerajinan:

  Segitiga sering digunakan dalam seni dan kerajinan, seperti origami, quilting, dan mosaik.

• D. Navigasi:

  Konsep segitiga digunakan dalam navigasi, seperti menghitung jarak dan arah.

• E. Geografi:

  Segitiga digunakan dalam peta dan survei untuk menentukan lokasi dan luas suatu daerah.

Kesimpulan

Memahami konsep luas dan keliling segitiga adalah keterampilan penting bagi siswa kelas 4. Dengan memahami definisi dasar, jenis-jenis segitiga, rumus perhitungan, dan tips mengerjakan soal, siswa dapat dengan mudah menyelesaikan berbagai soal yang berkaitan dengan segitiga. Selain itu, pemahaman tentang penerapan konsep segitiga dalam kehidupan sehari-hari akan membuat pembelajaran menjadi lebih menarik dan bermakna. Teruslah berlatih dan eksplorasi, dan Anda akan menjadi ahli dalam menguasai segitiga!

By adminAugust 4, 2025BlogLeave a Comment on Menguasai Segitiga: Luas dan Keliling untuk Kelas 4